در سلسه آموزش های مدارهای منطقی، قسمت نهم به تحلیل و بررسی مدارهای جمع کننده می پردازیم. مدارهای جمع کننده یکی از مهم ترین و پرکاربردترین مدار منطقی به کار می رود. در این قسمت به تحلیل و بررسی مدار نیم جمع کننده، یکی از مدارت مهم جمع کننده می پردازیم. مدار نیم جمع کننده پایه و اساس جمع در سیستم های دیجیتال را تشکیل می دهد. این مدار در ساختار داخلی خود از گیت های AND و XOR استفاده می کند. در این آموزش قصد داریم به تحلیل، بررسی و عملکرد این مدار بپردازیم. در ادامه با مرجع تخصصی الکترونیک به زبان فارسی، دیجی اسپارک همراه باشید.
تعریف و نحوه جمع اعداد باینری
پیش از معرفی مدار نیم جمع کننده، ابتدا نیاز است تا در رابطه با نحوه عمل جمع در مدارات دیجیتال، بدانیم. همانطور که اطلاع دارید، در مدارات دیجیتال عمل جمع به صورت باینری صورت می گیرد. فرض کنید قصد داریم دو عدد تک بیتی را با هم جمع کنیم. حتما می دانید که این اعداد می توانند ۰ یا ۱ را در خود ذخیره داشته باشند. یکی از این اعداد را A و دیگری را B می نامیم. جدول زیر جمع حالات مختلف این اعداد را در متغیر C، ذخیره می کند.
| C | B | A |
| ۰ | ۰ | ۰ |
| ۱ | ۱ | ۰ |
| ۱ | ۰ | ۱ |
| ۰ | ۱ | ۱ |
مطابق جدول فوق، جمع عدد ۰ با ۰، صفر خواهد بود. همچنین جمع عدد ۰ با ۱، یک خواهد بود. تنها مورد خاص، جمع دو عدد ۱ با ۱ بوده که حاصل آن، ۰ می شود!!!!. این موضوع مربوط به رقم نقلی می شود. رقم نقلی زمانی ایجاد می شود که حاصل جمع از تعداد بیت ها بیشتر شود. به عنوان مثال، فرض کنید دو عدد ۷ و ۸ را قصد داریم جمع کنیم. حاصل این جمع ۱۵ خواهد شد. همانطور که از ریاضیات ابتدایی به خاطر داریم، چون حاصل این جمع بیش از ۱۰ می شود، پس یک رقم دهگان ایجاد می شود. در محاسبات باینری هم این رقم دهگان که از آن به نام رقم نقلی(رقمی که از یک بیت به بیت دیگر متقل می شود) وجود دارد. چون حاصل جمع عدد یک با عدد یک دو شده و این عدد در باینری به صورت ۱۰ خواهد بود، لذا حاصل جمع دو عدد یک بیتی که هر دو یک هستند، رقم نقلی(مشابه دهگان) تولید می کند. بنابراین در جمع اعداد، دو خروجی زیر را داریم.
- حاصل جمع
- رقم نقلی
در قسمت بعدی به این موضوعات بیشتر می پردازیم.
جدول صحت و مدار منطقی نیم جمع کننده
پس از بررسی مبانی جمع باینری، نوبت به بررسی جدول صحت مدار نیم جمع کننده می رسد. در ابتدا به جدول زیر دقت کنید. در این جدول دو عدد A و B با هم جمع می شوند. سپس دو خروجی sum و carry، به ترتیب نتیجه محاسبات و رقم نقلی را در خود ذخیره می کنند.
| CARRY | SUM | B | A |
| ۰ | ۰ | ۰ | ۰ |
| ۰ | ۱ | ۱ | ۰ |
| ۰ | ۱ | ۰ | ۱ |
| ۱ | ۰ | ۱ | ۱ |
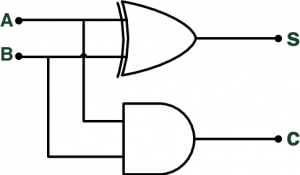
به خروجی های جدول فوق دقت کنید. خروجی SUM زمانی برابر با یک است که ورودی ها مخالف هم باشند. این دقیقا همان تعریف گیت XOR است. در کنار این، جالب است که به خروجی CARRY هم دقت کنید. خروجی CARRY تنها زمانی یک است که هر دو ورودی یک باشند. این مورد دقیقا تعریف گیت AND است. بدین ترتیب یک مدار نیم جمع کننده که پایه و اساس مدارت محاسباتی میکروکنترلرها و پردازنده را تشکیل می دهد؛ از یک گیت XOR برای نتیجه محاسبات و گیت AND برای رقم نقلی تشکیل شده است. تصویر زیر مدار داخلی نیم جمع کننده را نمایش می دهد.
مدارات نیم جمع کننده بسیار پایه ای بوده و تنها قادر به جمع دو بیت هستند. زمانیکه تعداد بیتهای اعداد زیاد تر شوند؛ این مدارت عملکرد نخواهند داشت. در این شرایط می بایست از چندین مدار نیم جمع کننده برای اجرای جمع استفاده نمود. در آموزش بعدی به این موضوع خواهیم پرداخت.
جمع بندی
در سلسله آموزش های تحلیل و بررسی مدارهای دیجیتال، قسمت نهم به بررسی مدار نیم جمع کننده پرداختیم. مدار نیم جمع کننده یکی از پایه ای ترین و پرکاربردترین مدار در سیستم های محاسباتی دیجیتال به شمار می رود. این مدار در واحدهای محاسبه گر میکروکنترلرها و میکروپروسسورها به کار می رود. این آموزش را با نحوه جمع باینری شروع کردیم. سپس به تحلیل و بررسی و مدار نیم جمع کننده پرداختیم. پس از اطلاع از نحوه اجرای جمع، به جدول صحت و مدار منطقی آن پرداختیم. در این آموزش آموختیم که مدار نیم جمع کننده از یک گیت XOR و AND تشکیل شده است. مدار نیم جمع کننده بسیار پایه ای بوده و جمع اعداد با تعداد بیت های بالاتر را نمی تواند انجام دهد. در چنین حالتی از چند مدار نیم جمع کننده باید استفاده نمود که موضوع بحث قسمت بعد و پایانی است.
چنانچه مطالب این آموزش را گنک یافتید، بدون هیچ نگرانی در انتهای همین پست، به صورت ثبت نظر سوالتان را مطرح کنید. من در سریعترین زمان ممکن پاسخ رفع مشکل شما را خواهم داد. همچنین اگر ایرادی در مطالب درج شده وجود دارد میتوانید از همین طریق اطلاع رسانی کنید.